پارداوکس تیر

زنون ایلیایی (تقریبا 500-600 سال قبل از میلاد) اولین اندیشمندی بود که به صورت جدی به بی نهایت کوچکها فکر کرد. او اعتقاد داشت که حرکت و تغییر در عالم واقع وجود ندارد و این دو مفهوم تنها توهمهایی هستند که توسط ذهن و احساس ما ساخته می شوند. زنون برای اثبات حرفهای خود استدلال هایی را مطرح کرد که امروزه آنها را به نام پارداوکسهای زنون می شناسیم. پارادوکس تیر یکی از این پارادوکس ها است. فیلم زیر را درباره پاردادوکس تیر ببینیم:

هندسه اقلیدسی چیست؟

هندسیه اقلیدسی چیست؟ پادکستی درباره ریشه های تاریخی و بنیانهای فلسفی هندسه اقلیدسی و محدودیتهای ذاتی آن. پادکست را از اینجا گوش کنید. 

طراحی های هندسی در کشورهای اسلامی

طراحی گره چینی در کشورهای مختلف رواج دارد اما در معماری اسلامی کاربرد گسترده ای پیدا کرده است. فیلم زیر در اینباره است.

تخت آباد

یه لحظه چشماتو ببند و فرض کن که توی دنیایی هستی کاملا مشابه دنیای ما فقط با یه تفاوت: توی اون دنیا همه چیز دو بعدی باشه نه سه بعدی. چه اتفاقی می افته؟

اولین اتفاقی که می افته اینه که دیگه نمیتونی بری توی خونه ت. چرا؟ به این دلیل ساده که میتونی کلید رو بکنی توی قفل ولی نمی تونی بچرخونی ش. برای اینکه کلید توی قفل بچرخه باید توی فضای سه بعدی باشیم. حالا سوال اینه که میشه قفلی درست کرد که کلیدش دو بعدی باشه؟

البته سوالات دیگری هم میشه مطرح کرد. مثلا موتور ماشین میشه درست کرد؛ یعنی ساختن سیلندر و پیستون امکان پذیره ولی برای انتقال نیرو به خارج از موتور نیاز به میل لنگ هست و میل لنگ هم فقط در فضای سه بعدی میتونه کار بکنه. پس یعنی موتورهای درون سوز پیستونی توی این دنیای فرضی کارآیی ندارن. اما بغیر از موتورهای پیستونی میشه توی دنیای  دو بعدی موتورهای درون سوز دیگری هم طراحی کرد؟

یا اینکه توی این دنیا اگر در خونه رو باز کردی پنجره ش رو هم می تونی باز کنی؟توجه کنید که توی این دنیا نمیشه زیر سقفها ستون زد چون اگه ستون بزنی کسی نمیتونه از این طرف ستون بره اون طرفش. حالا یه خونه مثل شکل زیر رو در نظر بگیرید که دریچه ی سمت چپ و دریچه ی سمت راست پنجره باشه. خوب اگه جفتش با هم باز بشه سقف خونه میاد روی سرت پایین.

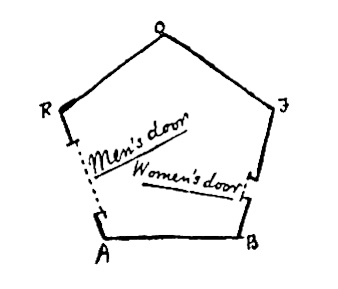
کشتی ها در این دنیا چگونه حرکت می کنند؟ همانند کلید قفل در حرکت کردن پروانه کشتی هم نیاز به سه بعد دارد پس آیا میشه مثلا کشتی های بادبونی در این جهان داشت.

قانون جاذبه در این دنیا چه صورتی دارد؟ آیا نیروی جاذبه همچنان با دو برابر شدن فاصله یک چهارم میشود؟ آیا رابطه نیرو و عکس مربع فاصله همچنان برقرار است؟ اقمار یه ستاره در چه مسیری دور اون میگردن.

سوالات وقتی جذاب تر میشن که فرض کنیم این جهان دو بعدی در دل یه فضای سه بعدی باشه و بعضی از اشکال سه بعدی امکان این رو داشته باشن که  وارد این جهان دوبعدی بشن. مثلا اگر یه دایره بخواد وارد جهان دو بعدی بشه از چشم مردم این جهان چه جوری دیده میشه؟ خوب اگر فقط یه نقطه ش با جهان دو بعدی مماس باشه به شکل نقطه دیده میشه ولی اگر بیشتر وارد بشه به صورت یه دایره دیده میشه. اگر یه کله قند از فضای سه بعدی وارد جهان دو بعدی بشه بسته به اینکه چه زاویه ای داشته باشه به صورت نقطه، دایره، بیضی، هذلولی و یا سهمی ممکنه دیده بشه. حالا اگه این اشکال سه بعدی بخوان درباره ی دنیای خودشون با مردم جهان دو بعدی صحبت کنن اونها چه برداشتی ممکنه داشته باشن؟

یه همچین سوالاتی ذهن یه ریاضی دان قرن نوزدهم به نام ادوین ابوت رو درگیر کرده بود. ابوت یه رمان فانتزی درباره ی جهانی فرضی می نویسه و اسمش رو میذاره : فلت لند رمانی درباره ی جهان های چند بعدی. این کتاب در سال 1884 منتشر شد و خودش منبع الهام برای تعداد دیگه ای از نوشته ها و فیلمهای فانتزی شد که به مسائل مختلف در جهانهای دو بعدی، سه بعدی و چهار بعدی می پرداختند. فلت لند رو میشه زمین مسطح یا دنیای مسطح فرض کرد ولی من ترجیح میدم بجاش بذارم : تخت آباد.

فیلم زیر یکی از انیمیشینهایی هست که با الهام از  داستان جذاب فلت لند ساخته شده. تفریح خوبی در ایام کرونایی عید که نمیتونی جایی بری دید و بازدید بشینی و این رو ببینی و یه مقداری درباره ش فکر کنی.

اصل رمان رو هم میتونی از اینجا دانلود ش کنی.